Deep MNIST for Beginners コード解説

学生時代は機械学習ツールがそれほど整備されておらず自力で実装することも多かったです。今はAIブームで手軽に試せるフレームワークやクラウドサービスが整ってて楽ですね。

久々に機械学習の進歩を追いかけるべく、まずはTensorFlowを試してみよう。

TensorFlow：Deep Learning MNIST手書き文字認識
https://www.tensorflow.org/get_started/

概要

MNIST手書き文字

対象となるMNIST手書き文字データは0〜9の10種類の文字である。ビギナー編ではまず古典的な単純パーセプトロンを用いた多クラス分類問題としてこれを解く。つまり入力された28x28の画像データが0〜9のどの文字かに分類する。

ニューラルネットワーク設計

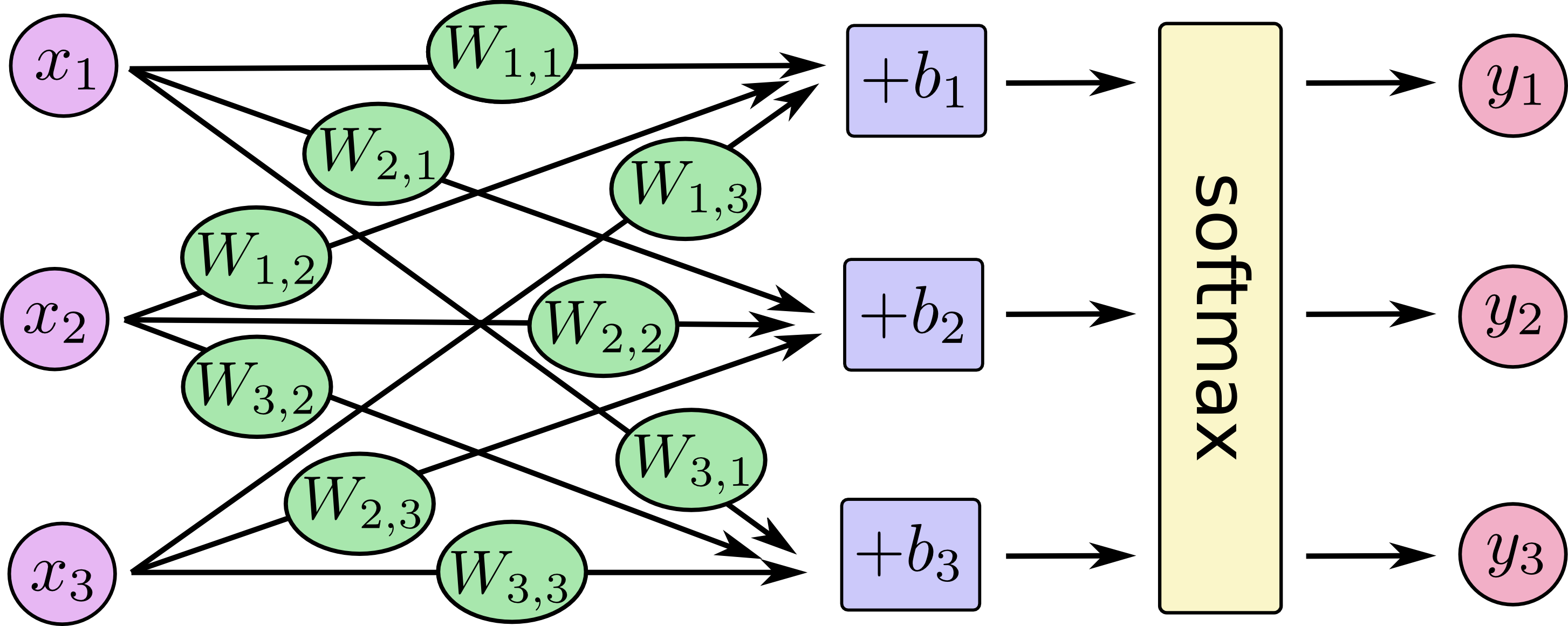
画像データ（28x28）の画素を一列に並べると784次元のベクトルとなる。 $x_{1}, x_{2},...,x_{784}$ が各画素に相当し、 $y_{0},y_{1},...,y_{9}$ が認識される数字の確率となる。図では簡略化のため、 $x,y$ の要素が３つの場合を描いている。

演算方法は単純で、各画素の値に重み $W_{i,j}$ を掛けてバイアス $b$ を足している。本家の解説から少し変えて、横ベクトルと行列で表してみる。

${\displaystyle y = \mbox{softmax} \begin{pmatrix} xW + b \end{pmatrix} \tag{1} }$

${\displaystyle \begin{bmatrix} y_{1}&y_{2}&y_{3} \end{bmatrix} = \mbox{softmax} \begin{pmatrix} \begin{bmatrix} x_{1}&x_{2}&x_{3} \end{bmatrix} \begin{bmatrix} W_{1,1}&W_{2,1}&W_{3,1} \\ W_{1,2}&W_{2,2}&W_{3,2} \\ W_{1,3}&W_{2,3}&W_{3,3} \end{bmatrix} + \begin{bmatrix} b_{1}&b_{2}&b_{3} \end{bmatrix} \end{pmatrix} \tag{2} }$

今回は出力 $y$ を確率にするため活性化関数としてsoftmax関数を利用する。softmax関数は出力を指数関数で正の値にし、総和が１になるように正規化している。

${\displaystyle y_k = \frac{e^{u_k}}{\sum_{m=1}^{K} e^{u_m}} \tag{3} }$

学習

このニューラルネットワークでの未知なパラメータは重み $W_{i,j}$ とバイアス $b$ である。学習とは入力と対応する正解データを与えて未知なパラメータを推定することを指す。正解データを与えて推定することを特に、教師あり学習とも呼ぶ。さて、パラメータを推定するには基準が必要となる。そこで正解と出力の誤差関数（損失関数とも呼ぶ）を定義し、これを最小化するパラメータを得ることにする。出力は確率なので確率分布の類似度を測るクロスエントロピーを誤差関数として利用できそうである。
正解ラベル $l$ 、出力 $y$ として誤差関数 $E$ をクロスエントロピーで定義する。誤差関数 $E$ を最小にする最適なパラメータを勾配法で解いて得ればよい。

${\displaystyle E(l,y)=-\sum_k l_k \log y_k \tag{4} }$

合成関数の微分を利用して誤差関数 $E$ を重み $W_{i,j}$ 、バイアス $b$ について偏微分してみる。

${\displaystyle \frac{\partial E}{\partial W_{k,j}} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial u_k} \frac{\partial u_k}{\partial W_{k,j}} \tag{5} }$

${\displaystyle \frac{\partial E}{\partial b_k} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial u_k} \frac{\partial u_k}{\partial b_k} \tag{6} }$

$\frac{\partial E}{\partial y_k}$ は式(4)から得られる。

${\displaystyle \frac{\partial E}{\partial y_k} = -\sum_k \frac{l_k}{y_k} \tag{7} }$

$\frac{\partial y_k}{\partial u_k}$ は式(3)から積の導関数の公式を利用して得られる。

${\displaystyle \sum_{m=1}^{K} e^{u_m} = \sum \mbox{と置くと、} y_k = \frac{e^{u_k}}{\sum_{m=1}^{K} e^{u_m}} = \frac{e^{u_k}}{\sum} \tag{8} }$

${\displaystyle \begin{align} \frac{\partial y_{k'}}{\partial u_k} &= \frac{\partial}{\partial u_k} \cdot \frac{e^{u_k}}{\sum} \\ &= \frac{e^{u_k}\sum - e^{u_k}e^{u_k}}{\sum^2} \\ &= \frac{e^{u_k}}{\sum} \cdot \frac{\sum - e^{u_k}}{\sum} \\ &= y_k (1-y_k) & (k'=k\mbox{ の場合}) \end{align} \tag{9} }$

${\displaystyle \begin{align} \frac{\partial y_{k'}}{\partial u_k} &= \frac{\partial}{\partial u_k} \cdot \frac{e^{u_k}}{\sum} \\ &= -\frac{e^{u_{k'}}e^{u_k}}{\sum^2} \\ &= -y_{k'} y_k & (k' \neq k\mbox{ の場合}) \end{align} \tag{10} }$

これらは自明である。

${\displaystyle \frac{\partial u_k}{\partial W_{k,j}} = x_j \tag{11} }$

${\displaystyle \frac{\partial u_k}{\partial b_k} = 1 \tag{12} }$

$\frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial u_k}$ は整理すると簡単になる。

${\displaystyle {\frac{\partial E}{\partial y_{k'}} \frac{\partial y_{k'}}{\partial u_k} = -\sum_{k'} \frac{l_{k'}}{y_{k'}} \frac{\partial y_{k'}}{\partial u_k} = - l_k(1-y_k) + \sum_{k'\neq k} l_{k'} y_k = - l_k + y_k \sum_{k'} l_{k'} = y_k - l_k } \tag{13} }$

ここまでの式により、最急降下法の更新式を得る。収束係数 $\alpha$ は(0.0〜1.0)の値を設定する。

${\displaystyle W_{k,j}^{new} \leftarrow W_{k,j}^{old} - \alpha \frac{\partial E}{\partial W_{k,j}} = W_{k,j}^{old} - \alpha (y_k - l_k) x_j \tag{14} }$

${\displaystyle b_k^{new} \leftarrow b_k^{old} - \alpha \frac{\partial E}{\partial b_k} = b_k^{old} - \alpha (y_k - l_k) \tag{15} }$

コード解説

コード全容

処理は①〜⑩の順に実行される。

# Copyright 2015 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================

"""A very simple MNIST classifier.

See extensive documentation at
https://www.tensorflow.org/get_started/mnist/beginners
"""

# ①
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

FLAGS = None


def main(_):
  # ④Import data
  mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)

  # ⑤Create the model
  x = tf.placeholder(tf.float32, [None, 784])
  W = tf.Variable(tf.zeros([784, 10]))
  b = tf.Variable(tf.zeros([10]))
  y = tf.matmul(x, W) + b

  # ⑥
  y_ = tf.placeholder(tf.float32, [None, 10])

  # The raw formulation of cross-entropy,
  #
  #   tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(tf.nn.softmax(y)),
  #                                 reduction_indices=[1]))
  #
  # can be numerically unstable.
  #
  # So here we use tf.nn.softmax_cross_entropy_with_logits on the raw
  # outputs of 'y', and then average across the batch.
  # ⑦Define loss and optimizer
  cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
  train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

  # ⑧
  sess = tf.InteractiveSession()
  tf.global_variables_initializer().run()

  # ⑨Train
  for _ in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

  # ⑩Test trained model
  correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
  print(sess.run(accuracy, feed_dict={x: mnist.test.images,
                                      y_: mnist.test.labels}))

if __name__ == '__main__':
  # ②
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()
  
  # ③
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

ライブラリインポート

# ①
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

FLAGS = None

from __future__はpython3の機能のインポート。あとは必要なライブラリとtensorflowのライブラリを読み込んでいる。FLAGSはパースした引数の格納に使われる。

引数のパース

if __name__ == '__main__':
  # ②
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()

mnistのテストデータの一時保存先ディレクトリを引数で指定でき、特に指定がなければ'/tmp/tensorflow/mnist/input_data'が使用されることになる。結果はグローバル変数のFLAGSに格納される。

tensorflowアプリケーションの実行

  # ③
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

tf.app.runは残りの引数をパースして渡したメソッドを実行してくれるヘルパー関数である。なので、直接mainメソッドを呼び出しても変わらない。なお、パースした引数は以下のようにアクセスできる。

from tensorflow.python.platform import flags
f = flags.FLAGS
f.key    # keyはパースされた引数名

mnistデータ読み込み

def main(_):
  # ④Import data
  mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)

mnistのデータをダウンロードして読み込んでくれる。もちろん、本来なら自分でデータセットを用意して読み込むことになる。

モデルの作成

  # ⑤Create the model
  x = tf.placeholder(tf.float32, [None, 784])
  W = tf.Variable(tf.zeros([784, 10]))
  b = tf.Variable(tf.zeros([10]))
  y = tf.matmul(x, W) + b

ここでもう一度、式を見てみよう。式の計算通りであることがわかる。
${\displaystyle y = \mbox{softmax} \begin{pmatrix} xW + b \end{pmatrix} \tag{1} }$
tf.placeholderは、学習／識別計算時に与えられることを宣言している。第二引数[None, 784]は二階テンソルで、１軸目の次元数が可変、２軸目が784次元であることを示す（つまり、N×784の行列）。１軸目は入力画像数なので、任意の数の画像を一度に学習／識別が可能となる。
ところで、tf.matmul(x, W)の計算結果はN×10のテンソルだが、バイアスベクトル $b$ は階数が異なるため足せないように見える。これはブロードキャストという仕組みにより、バイアスベクトル $b$ はN×10のテンソルに自動拡張され計算できるようにしてくれる（各行は元の $b$ のコピー）。詳細は他所に譲る。

トレーニング用の正解ラベル

# ⑥
  y_ = tf.placeholder(tf.float32, [None, 10])

教師あり学習として解くため、正解ラベルを設定するプレースホルダを宣言している。

損失関数とオプティマイザ

  # The raw formulation of cross-entropy,
  #
  #   tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(tf.nn.softmax(y)),
  #                                 reduction_indices=[1]))
  #
  # can be numerically unstable.
  #
  # So here we use tf.nn.softmax_cross_entropy_with_logits on the raw
  # outputs of 'y', and then average across the batch.
  # ⑦Define loss and optimizer
  cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
  train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

各入力画像のクロスエントロピーの平均値を最小化するため、これを最急降下法で解く計算グラフをtrain_stepとして定義している。クロスエントロピーを理論どおりに実装すると指数を扱う関係で場合によってはオーバーフローを起こすため、TensorFlowで用意されているtf.nn.softmax_cross_entropy_with_logits()を利用する。

セッションの生成と初期化

  # ⑧
  sess = tf.InteractiveSession()
  tf.global_variables_initializer().run()

TensorFlowの実際の計算は、C++で作られたバックエンドに依存している（バックエンドからCPU/GPUがゴリゴリ使用される）。Python上ではテンソルの計算グラフを定義し、セッションと呼ばれるバックエンドとのコネクションを通じて計算を実行していることになる。なぜこのような仕組みになっているかというと、途中経過を含む計算結果を毎回Pythonの変数にバインドするのはオーバーヘッドが大きすぎるため、計算グラフをバックエンド内に閉じて実行しているのである。
InteractiveSessionはその名の通りインタラクティブなので、セッション生成前に定義した計算グラフだけでなく、生成後に追加で計算グラフを定義・実行ができる。global_variables_initializerは、それまでに定義した変数、今回だとW,bを初期化している。

学習

  # ⑨Train
  for _ in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

学習では、sess.run()で定義した計算グラフtrain_stepを実行している。train_stepの計算グラフを辿ると、２つのプレースホルダxとy_があったことを思い出してほしい。プレースホルダは実行時に値を与えなければならない。そこで引数feed_dictでこれらを与えている。
学習においてトレーニングデータの与え方もいくつかあるが、今回はミニバッチを用いている。ミニバッチとはトレーニングデータから任意の数のデータをランダムに選択・学習を繰り返す手法である。ここでは、トレーニングデータから100個ランダムに選択して学習する処理を1000回繰り返している。

学習結果の認識精度テスト

  # ⑩Test trained model
  correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
  print(sess.run(accuracy, feed_dict={x: mnist.test.images,
                                      y_: mnist.test.labels}))

学習が完了したら認識精度テストを実行する。精度は正解数の平均値として定義している。tf.argmax(y, 1)は、テンソルyの各行の最大値のインデックスを返す。正解y_と予測yが一致するなら同じインデックスを指すはずなので、tf.equalはtrueかfalseを返す。tf.reduce_mean(tf.cast(correct_prediction, tf.float32))でboolをfloat32に変換（true -> 1.0, false -> 0.0）し、平均値を算出している。
なおsoftmax関数は単調増加なので、ここでは予測yにsoftmax関数を適用しなくても問題ない。具体的な確率を表示させたい場合は、tf.nn.softmax(y)を出力する。